Системы трёх линейных уравнений с тремя неизвестными

Системы трёх линейных уравнений с тремя неизвестными.

Основные  методы решения: подстановка, сложение или вычитание .

Определители третьего порядка. Правило Крамера.

Системы трёх линейных уравнений с тремя неизвестными имеют вид:

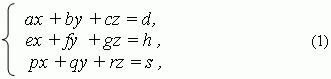
где a , b , c , d , e , f , g , h , p , q , r , s – заданные числа; x , y , z – неизвестные. Числа a , b , c , e , f , g , p , q , r – коэффициенты при неизвестных ; d , h , s – свободные члены . Решение этой системы может быть найдено теми же двумя основными методами, рассмотренными выше: подстановки и сложения или вычитания. Мы же рассмотрим здесь подробно только метод Крамера.

Во-первых, введём понятие определителя третьего порядка . Выражение

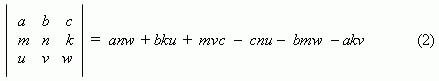
называется определителем третьего порядка.

Запоминать это выражение не нужно, так как его легко получить, если переписать таблицу (2), добавив справа первые два столбца. Тогда оно вычисляется путём перемножения чисел, расположенных на диагоналях, идущих от a , b , c – направо ( со знаком « + » ) и от c , a , b – налево ( со знаком «  – » ), и затем суммированием этих произведений:

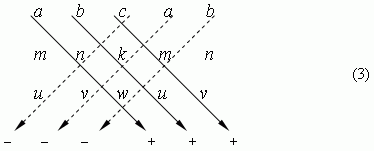
Используя определитель третьего порядка (2), можно получить решение системы уравнений (1) в виде:

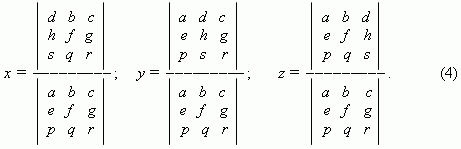
Эти формулы и есть правило Крамера для решения системы трёх линейных уравнений с тремя неизвестными.

П р и м е р .  Решить методом Крамера систему трёх линейных уравнений с тремя неизвестными:

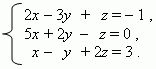
Р е ш е н и е .  Введём следующие обозначения: D - знаменатель в формулах (4),

Dx , Dy , Dz – числители в выражениях для x , y , z – соответственно.

Тогда используя схему (3), получим:

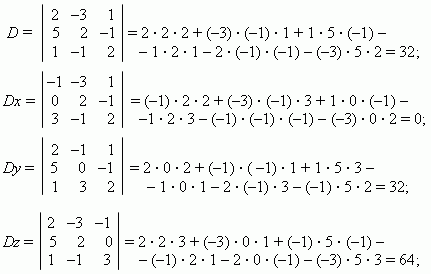
отсюда по формулам Крамера (4): x = Dx / D = 0 / 32 = 0;

y = Dy / D = 32 / 32 = 1; z = Dz / D = 64 / 32 = 2 .

Назад