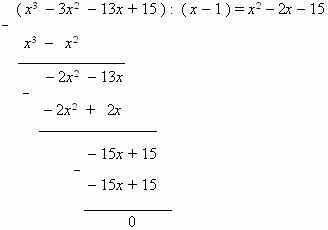Уравнения высших степеней

Уравнения высших степеней, приводимые к квадратному.

Биквадратное уравнение. Кубическое уравнение .

1.

Некоторые виды уравнений высших степеней можно решить, используя квадратное уравнение. Иногда можно разложить левую часть уравнения на множители, каждый из которых является многочленом не выше второй

степени. Тогда, приравнивая каждый из них к нулю и решая все эти квадратные и / или линейные уравнения, мы получим все корни исходного уравнения.

П р и м е р .  Решить уравнение:  3 x 4 + 6 x 3 – 9 x 2 = 0 .

Р е ш е н и е .  Разложим левую часть этого уравнения на множители:

x 2 ( 3 x 2 +  6 x –  9 ) .

Решим уравнение: x 2 = 0; оно имеет два корня: x 1 = x 2 = 0 .

Теперь решим уравнение: 3 x 2 + 6 x – 9 = 0,  и получим:

x 3 = 1  и x 4 = – 3 .

Таким образом, исходное уравнение имеет четыре корня:

x 1 = x 2 = 0 ; x 3 = 1 ; x 4 = – 3 .



2.

Если уравнение имеет вид:

ax 2 n + bx n +  c = 0  ,

оно приводится к квадратному уравнению заменой:

x n = z ;

действительно, после этой замены получаем: az 2 + bz + c = 0 .

П р и м е р .  Рассмотрим уравнение:

x 4 – 13 x 2 + 36 = 0 .

После замены: x 2 = z получим уравнение:

z 2 – 13 z + 36 = 0 .

Его корни: z 1 = 4  и z 2 = 9. Теперь решаем  уравнения:

x 2 = 4 и x 2 = 9 . Они имеют соответственно корни:

x 1 = 2 , x 2 = – 2 , x 3 = 3 ; x 4 = – 3 .  Эти числа являются

корнями исходного уравнения ( проверьте, пожалуйста! ).

Любое уравнение вида: ax 4 + bx 2 + c = 0 называется биквадратным .

Оно приводится к квадратному уравнению заменой:

x 2 = z .

П р и м е р .  Решить биквадратное уравнение:  3 x 4 – 123 x 2 + 1200 = 0 .

Р е ш е н и е .  Заменяя: x 2 = z , и решая уравнение:

3 z 2 – 123 z + 1200 = 0, получаем:

отсюда, z 1 = 25 и z 2 = 16. Используя нашу замену, получим:

x 2 = 25 и x 2 = 16,  отсюда, x 1 = 5, x 2 = – 5, x 3 = 4, x 4 = – 4.



3. Кубическое уравнение – это уравнение третьей степени вида:

ax 3 + bx 2 + cx + d = 0 .

Известные формулы Кардано для решения уравнений этого типа очень сложны и почти не применяются на практике. Поэтому мы рекомендуем другой путь для решения уравнений третьей степени.
1).

Сначала путём перебора найдём один из корней уравнения. Дело в том, что кубические уравнения всегда имеют по крайней мере один действительный корень, причем целый корень кубического уравнения с целыми коэффициентами является делителем свободного члена d . Коэффициенты этих уравнений обычно подобраны так, что искомый корень лежит среди небольших целых чисел, таких как:  0, ± 1, ± 2, ± 3. Поэтому мы будем искать корень среди этих чисел и проверять его путём подстановки в уравнение. Вероятность успеха при таком подходе очень высока. Предположим, что этот корень x 1 .

2).

Вторая стадия решения – это деление многочлена ax 3 + bx 2 + cx + d на двучлен x – x 1 . Согласно теореме Безу (см. раздел «Деление многочлена на линейный двучлен») это деление без остатка возможно, и мы получим в результате многочлен второй степени, который надо приравнять к нулю. Решая полученное квадратное уравнение, мы найдём (или нет!) оставшиеся два корня.

П р и м е р .  Решить уравнение: x 3 – 3 x 2 – 13 x + 15 = 0 .

Р е ш е н и е .  Ищем первый корень перебором чисел: 0, ± 1, ± 2, ± 3

и подстановкой в уравнение. В результате находим,

что 1 является корнем. Тогда делим левую часть этого

уравнения на двучлен x – 1,  и получаем:

Теперь, решая квадратное уравнение: x 2 – 2 x – 15 = 0,

находим оставшиеся два корня: x 1 = – 3  и x 2 = 5 .

Назад