Комплексные числа

Мнимые и комплексные числа. Абсцисса и ордината

комплексного числа. Сопряжённые комплексные числа.

Операции с комплексными числами. Геометрическое

представление комплексных чисел. Комплексная плоскость.

Модуль и аргумент комплексного числа. Тригонометрическая

форма комплексного числа. Операции с комплексными

числами в тригонометрической форме. Формула Муавра.

Начальные сведения о мнимых и комплексных числах приведены в разделе «Мнимые и комплексные числа». Необходимость в этих числах нового типа появилась при решении квадратных уравнений для случая D < 0 ( здесь D – дискриминант квадратного уравнения). Долгое время эти числа не находили физического применения, поэтому их и назвали «мнимыми» числами. Однако сейчас они очень широко применяются в различных областях физики

и техники: электротехнике, гидро- и аэродинамике, теории упругости и др.

Комплексные числа записываются в виде: a + bi . Здесь a и b – действительные числа , а i – мнимая единица, т. e . i ² = –1. Число a называется абсциссой , a b – ординатой комплексного числа a + bi . Два комплексных числа a + bi и a – bi называются сопряжёнными комплексными числами.

Основные договорённости:

1.  Действительное число а может быть также записано в форме комплексного числа: a + 0 i или a – 0 i . Например, записи  5 + 0 i и  5 – 0 i означают одно и то же число 5 .

2.  Комплексное число 0 + bi называется чисто мнимым числом . Запись bi означает то же самое, что и  0 + bi .

3.  Два комплексных числа a + bi и c + di считаются равными, если a = c и b = d . В противном случае комплексные числа не равны.

Сложение. Суммой комплексных чисел a + bi и c + di называется комплексное число ( a + c ) + ( b + d ) i . Таким образом, при сложении комплексных чисел отдельно складываются их абсциссы и ординаты.

Это определение соответствует правилам действий с обычными многочленами.

Вычитание. Разностью двух комплексных чисел a + bi (уменьшаемое) и c + di (вычитаемое) называется комплексное число ( a – c ) + ( b – d ) i .

Таким образом, при вычитании двух комплексных чисел отдельно вычитаются их абсциссы и ординаты.

Умножение. Произведением комплексных чисел a + bi и c + di называется комплексное число:

( ac – bd ) + ( ad + bc ) i . Это определение вытекает из двух требований:

1)  числа a + bi и c + di должны перемножаться, как алгебраические двучлены,

2)  число i обладает основным свойством: i ² = – 1.

П р и м е р .  ( a+ bi )( a – bi ) = a ² + b ² . Следовательно, произведение

двух сопряжённых комплексных чисел равно действительному

положительному числу.

Деление. Разделить комплексное число a + bi (делимое) на другое c + di (делитель) - значит найти третье число e + f i (частное), которое будучи умноженным на делитель c + di ,  даёт в результате делимое a + bi .

Если делитель не равен нулю, деление всегда возможно.

П р и м е р .  Найти  ( 8 + i ) : ( 2 – 3 i ) .

Р е ш е н и е . Перепишем это отношение в виде дроби:

Умножив её числитель и знаменатель на  2 + 3 i

и выполнив все преобразования, получим:

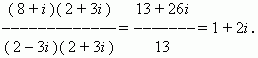
Геометрическое представление комплексных чисел. Действительные числа изображаются точками на числовой прямой:

Здесь точка A означает число –3, точка B – число 2, и O – ноль. В отличие от этого комплексные числа изображаются точками на координатной плоскости. Выберем для этого прямоугольные (декартовы) координаты с одинаковыми масштабами на обеих осях. Тогда комплексное число a + bi будет представлено точкой Р  с абсциссой а и ординатой b (см. рис.). Эта система координат называется комплексной плоскостью .

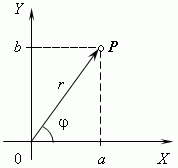
Модулем комплексного числа называется длина вектора OP , изображающего комплексное число на координатной ( комплексной ) плоскости. Модуль комплексного числа a + bi обозначается  | a + bi | или буквой r и равен:

Сопряжённые комплексные числа имеют одинаковый модуль. __

Аргумент комплексного числа - это угол между осью OX и вектором OP , изображающим это комплексное число. Отсюда, tan = b / a .

Тригонометрическая форма комплексного числа. Абсциссу a и ординату b комплексного числа a + bi можно выразить через его модуль r и аргумент :

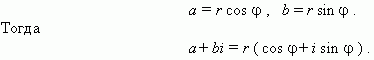
Операции с комплексными числами, представленными в тригонометрической форме.

Это знаменитая формула Муавра.

Здесь k - целое . Чтобы получить n различных значений корня n -ой степени из z необходимо задать n последовательных значений для k ( например, k = 0, 1, 2,…, n – 1 ) .