Арифметическая и геометрическая прогрессии

Числовая последовательность. Арифметическая прогрессия.

Разность прогрессии. Геометрическая прогрессия. Знаменатель

прогрессии. Бесконечно убывающая геометрическая прогрессия.

Обращение периодической десятичной дроби в обыкновенную.

Последовательности. Рассмотрим ряд натуральных чисел:

1,  2,  3, … , n – 1, n , … .

Если заменить каждое число n в этом ряду некоторым числом u _n , следуя некоторому закону, мы получим новый ряд чисел:

u ₁ , u ₂ , u ₃ , …, u _{n - 1} , u _n , … ,

называемый числовой последовательностью . Число u _n называется общим членом числовой последовательности.

П р и м е р ы   числовых последовательностей:

2,   4,   6,   8,   10,  … ,  2 n ,  … ;

1,   4,   9,   16,   25,  … , n ² , … ;

1,  1/2,  1/3,  1/4,  1/5,  … , 1/ n , … .

Арифметическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с постоянным для этой последовательности числом d , называется арифметической прогрессией . Число d называется разностью прогрессии . Любой член ариф метической прогрессии вычисляется по формуле:

Сумма n первых членов арифметической прогрессии вычисляется как:

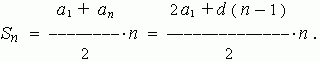
П р и м е р .  Найти сумму первых ста нечётных чисел.

Р е ш е н и е . Применим последнюю формулу. Здесь a ₁ = 1, d = 2 . Тогда

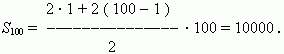
Геометрическая прогрессия. Числовая последовательность, каждый член которой, начиная со второго, равен предыдущему, умноженному на постоянное для этой последовательности число q , называется геометрической

прогрессией . Число q называется знаменателем прогрессии .  Любой член геометрической прогрессии вычисляется по формуле:

b _n =  b ₁ q ^{n - 1} .

Сумма n первых членов геометрической прогрессии вычисляется как:

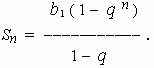
Бесконечно убывающая геометрическая прогрессия. Это геометрическая прогрессия, у которой  | q | < 1 . Для неё определяется понятие суммы членов бесконечно убывающей геометрической прогрессии , а именно:  это число, к

которому неограниченно приближается сумма n первых членов рассматри ваемой прогрессии при неограниченном возрастании числа n . Сумма членов бесконечно убывающей геометрической прогрессии вычисляется по формуле:

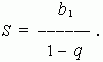
П р и м е р .  Найти сумму членов бесконечно убывающей геометрической прогрессии:

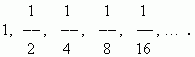
Р е ш е н и е . Применим последнюю формулу. Здесь b ₁ = 1, q = 1/2. Тогда:

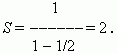
Обращение периодической десятичной дроби в обыкновенную. Предположим, мы хотим обратить периодическую десятичную дробь 0.(3)  в обыкновенную. Рассмотрим эту десятичную дробь в следующем виде:

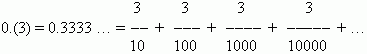
Это бесконечно убывающая геометрическая прогрессия, первый член которой равен 3/10, а разность q = 1/10. В соответствии с выше приведенной формулой эта сумма равна:

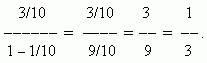
Таким образом ,  0.(3) = 1/3.