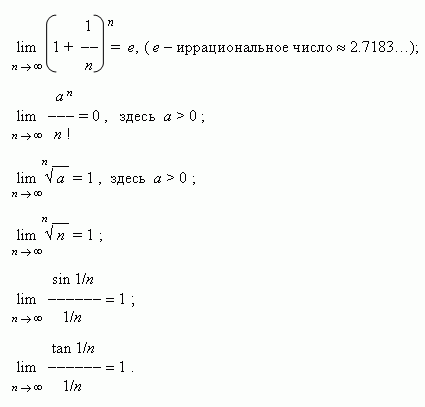Последовательности. Рассмотрим ряд натуральных чисел:

1,  2,  3, … , n –1, n , … .

Если заменить каждое натуральное число n в этом ряду некоторым числом u _n , следуя некоторому закону, то мы получим новый ряд чисел:

u ₁ , u ₂ , u ₃ , …, u _{n - 1} , u _n , …, кратко обозначаемый { u _n }

и называемый числовой последовательностью . Величина u _n называется общим членом последовательности. Обычно числовая последовательность задаётся некоторой формулой u _n = f ( n ), позволяющей найти любой член последовательности по его номеру n ; эта формула называется формулой общего члена. Заметим, что задать числовую последовательность формулой общего члена не всегда возможно; иногда последовательность задаётся путём описания её членов (см. ниже последний пример).

П р и м е р ы    числовых последовательностей:

1,  2,  3,  4,  5, … - ряд натуральных чисел ;

2,  4,  6,  8,  10, … - ряд чётных чисел;

1.4,  1.41,  1.414,  1.4142, … - числовая последовательность

приближённых  значений

с увеличивающейся точностью.

В последнем примере невозможно дать формулу общего члена последовательности, тем не менее эта последовательность описана полностью.

Предел числовой последовательности. Рассмотрим числовую последовательность, общий член которой приближается к некоторому числу a при увеличении порядкового номера n . В этом случае говорят, что числовая последовательность имеет предел . Это понятие имеет более строгое определение.

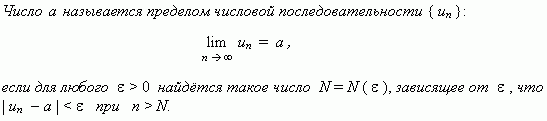
Это определение означает, что a есть предел числовой последовательности, если её общий член неограниченно приближается к a при возрастании n . Геометрически это значит, что для любого > 0 можно найти такое число N ,  что начиная с n > N все члены последовательности расположены внутри интервала ( a - , a + ). Последовательность, имеющая предел, называется сходящейся ; в противном случае – расходящейся .

Последовательность называется ограниченной , если существует такое число M , что | u _n | M для всех n . Возрастающая или убывающая последовательность называется монотонной .

Теорема Вейерштрасса. Всякая монотонная и ограниченная последовательность имеет предел (эта теорема даётся в средней школе без доказательства).

Основные свойства пределов. Нижеприведенные свойства пределов справедливы не только для числовых последовательностей, но и для функций.

Если { u _n } и { v _n } - две сходящиеся последовательности, то:

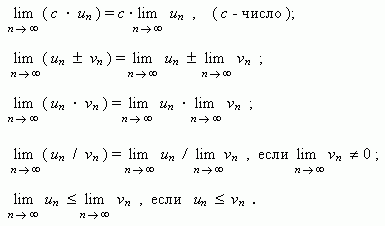
Если члены последовательностей { u _n }, { v _n }, { w _n } удовлетворяют неравенствам

Некоторые замечательные пределы.