Правило Лопиталя
Пусть при
x
a
для
функций
f
(
x
)
и
g
(
x
),
дифференцируемых
в неко
торой
окрестности точки
а
, выполняются условия:
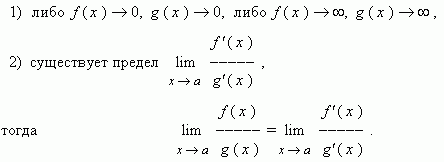
Эта теорема называется
правилом
Лопиталя
. Она позволяет
вычислять пределы отношения функций, когда и числитель, и знаменатель
c
тремятся
либо к нулю, либо к бесконечности. Правило Лопиталя, как говорят математики,
позволяет избавляться от неопределённостей типа:
0 / 0
и
/
.
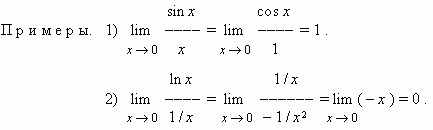
При
неопределённостях другого типа:
–
,
×
0
,
0
0
,
0
,
нужно проделать
предварительно ряд
тождественных
преобразований,
чтобы
привести
их
/
.
После
этого
можно применять правило Лопиталя. Покажем некоторые из возможных преобразований
указанных неопределённостей.
| 1) |
–
:
пусть f ( x )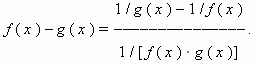
,
g
(
x
)
,
тогда
данная неопределённость приводится к типу 0 / 0
следующим преобразованием:
|
| 2) |
|
| 3) |
остальные неопределённости
приводятся к первым двум с помощью
логарифмического преобразования:
|
Если после применения правила Лопиталя
неопределённость типа 0 / 0 или
/
осталась, нужно применить его повторно. Многократное
применение правила Лопиталя может привести к требуемому результату.
Правило Лопиталя применимо и в случае, если
x
.