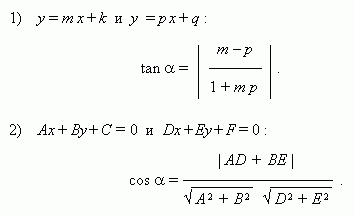Прямая
Общее уравнение прямой. Нормальный вектор.
Уравнение прямой с угловым коэффициентом.
Уравнение прямой в отрезках на осях. Уравнение прямой, проходящей
через две различные точки. Параметрическое уравнение прямой.
Условие параллельности прямых. Условие перпендикулярности прямых.
Расстояние между двумя точками . Расстояние от точки до прямой.
Расстояние между параллельными прямыми. Угол между прямыми.
Общее уравнение прямой:
Ах + Ву + С = 0 ,
где А и В не равны нулю одновременно.
Коэффициенты А и В являются координатами нормального вектора прямой ( т.е. вектора, перпендикулярного прямой ). При А = 0 прямая параллельна оси ОХ , при В = 0 прямая параллельна оси О Y .
При
В
0
получаем
уравнение прямой с угловым коэффициентом
:
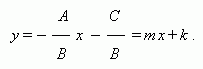
Уравнение прямой, проходящей через точку ( х 0 , у 0 ) и не параллельной оси OY , имеет вид:
у – у 0 = m ( x – х 0 ) ,
где m – угловой коэффициент , равный тангенсу угла, образованного данной прямой и положительным направлением оси ОХ .
При
А
0,
В
0 и
С
0
получаем
уравнение
прямой в отрезках на осях
:
где a = – C / A , b = – C / B . Эта прямая проходит через точки ( a , 0 ) и ( 0, b ), т.е. отсекает на осях координат отрезки длиной a и b .
Уравнение прямой, проходящей через две различные точки ( х
1 , у 1 ) и ( х 2 , у 2 ):
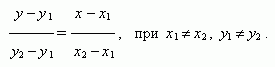
Параметрическое уравнение прямой , проходящей через точку ( х 0 , у 0 ) и парал лельной направляющему вектору прямой ( a , b ) :
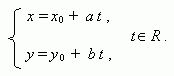
Условие параллельности прямых:
1) для прямых Ах+ Ву+ С = 0 и D х+ E у+ F = 0 : AE – BD = 0 ,
2) для прямых у = m x + k и у = p x + q : m = p .
Условие перпендикулярности прямых:
1) для прямых Ах+ Ву+ С = 0 и D х+ E у+ F = 0 : AD + BE = 0 ,
2) для прямых у = m x + k и у = p x + q : m p = – 1 .
Расстояние между двумя точками ( x 1 , y 1 ) и ( x 2 , y 2 ) :
Расстояние от точки ( х 0 , у 0 ) до прямой Ах+ Ву+ С = 0 :
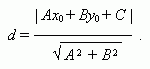
Расстояние между параллельными прямыми Ах+ Ву+ С = 0 и A х+ B у+ F = 0 :
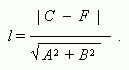
Угол
между прямыми:
