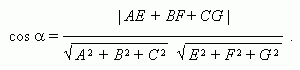Плоскость
Общее уравнение плоскости. Нормальный вектор.
Уравнение плоскости в отрезках на осях.
Уравнение плоскости, проходящей через заданную
точку и перпендикулярной заданному вектору.
Параметрическое уравнение плоскости.
Условие параллельности плоскостей.
Условие перпендикулярности плоскостей.
Расстояние между двумя точками.
Расстояние от точки до плоскости.
Расстояние между параллельными плоскостями.
Угол между плоскостями.
Общее уравнение плоскости:
Ах + Ву + С z + D = 0 ,
где А , B и C не равны нулю одновременно.
Коэффициенты А , B и C являются координатами нормального вектора плоскости ( т.е. вектора, перпендикулярного плоскости ).
При
А
0,
В
0,
С
0 и
D
0
получаем
уравнение плоскости
в отрезках на осях
:
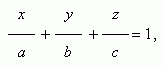
где a = – D / A , b = – D / B , c = – D / C . Эта плоскость проходит через точки ( a , 0, 0 ), ( 0, b , 0 ) и ( 0, 0, с ), т.е. отсекает на осях координат отрезки длиной a , b и c .
Уравнение плоскости , проходящей через точку ( х 0 , у 0 , z 0 ) и перпендикулярной вектору ( А , В, C ) :
А ( х – х 0 ) + В ( у – у 0 ) + С ( z – z 0 ) = 0 .
Параметрическое уравнение плоскости , проходящей через точку ( х 0 , у 0 , z 0 ) и два неколлинеарных вектора ( a 1 , b 1 , c 1 ) и ( a 2 , b 2 , c 2 ) , заданных в прямоугольной декартовой системе координат:
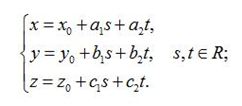
Условие параллельности плоскостей Ах+ Ву+ С z + D = 0 и E х + F у + Gz+ H = 0:
AF – BE = BG – CF = AG – CE = 0 .
Условие перпендикулярности плоскостей Ах+ Ву+ С z + D = 0 и E х+ F у+ Gz + H = 0:
А E + В F + С G = 0 .
Расстояние между двумя точками ( х 1 , у 1 , z 1 ) и ( x 2 , y 2 , z 2 ) :
Расстояние от точки ( х 0 , у 0 , z 0 ) до плоскости Ах + Ву + С z + D = 0 :
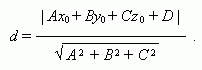
Расстояние между параллельными плоскостями Aх + By + Cz + D = 0 и Aх + By + Cz + Е = 0
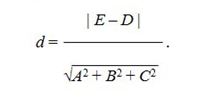
Угол
между
плоскостями
Ах+ Ву+ С
z
+
D
=
0 и
E
х+
F
у+
Gz
+
H
=
0:
