Десятичные дроби
Десятичная дробь. Целая часть. Десятичная точка.
Десятичные знаки. Свойства десятичных дробей.
Периодическая десятичная дробь. Период .
Десятичная дробь есть результат деления единицы на десять, сто, тысячу и т.д. частей. Эти дроби очень удобны для вычислений, так как они основаны на той же позиционной системе, на которой построены счёт и запись целых чисел. Благодаря этому запись и правила действий с десятичными дробями фактически те же, что и для целых чисел. При записи десятичных дробей нет необходимости отмечать знаменатель, это определяется местом, которое занимает соответствующая цифра. Сначала пишется целая часть числа, затем справа ставится десятичная точка . Первая цифра после десятичной точки означает число десятых, вторая – число сотых, третья – число тысячных и т.д. Цифры, расположенные после десятичной точки, называются десятичными знаками .
П р и м е р
.
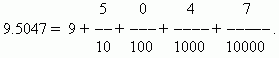
Одно из преимуществ десятичных дробей – они легко приводятся к виду обыкновенных: число после десятичной точки (в нашем случае 5047) – это числитель; знаменатель же равен n –ой степени 10, где n - количество десятичных знаков (в нашем случае n = 4):
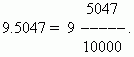
Если десятичная дробь не содержит целой части, то перед десятичной точкой ставится ноль:
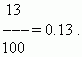
Свойства десятичных дробей.
1. Десятичная дробь не меняется, если справа добавить нули :
13.6 =13.6000.
2. Десятичная дробь не меняется, если удалить нули, расположенные
в конце десятичной дроби :
0.00123000 = 0.00123 .
Внимание! Нельзя удалять нули, расположенные не в конце десятичной дроби!
| 3. |
Десятичная дробь возрастает в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций вправо :
3.675 ---> 367.5 (дробь возросла в 100 раз). |
| 4. |
Десятичная дробь уменьшается в 10, 100, 1000 и т.д. раз, если перенести десятичную точку на одну, две, три и т.д. позиций влево :
1536.78 ---> 1.53678 (дробь уменьшилась в 1000 раз). |
Эти свойства позволяют быстро умножать и делить десятичные дроби на 10, 100, 1000 и т.д.
Периодическая десятичная дробь содержит бесконечно повторяющуюся группу цифр, называемую периодом . Период записывается в скобках. Например, 0.12345123451234512345… = 0.(12345).
П р и м е р . Если разделить 47 на 11, то получим 4.27272727… = 4.(27).