Координаты. Графическое представление функций
Координаты. Система координат. Декартовы координаты.
Оси координат: ось абсцисс , ось ординат. Начало
координат. Масштаб. Абсцисса и ордината точки.
Графическое представление функций. График функции.
Координаты. Две взаимно перпендикулярные прямые
XX ’ и YY ’ ( рис.1 ) образуют систему координат , называемых декартовыми координатами. Прямые XX ’ и YY ’ называются осями координат . Ось XX ’ называется осью абсцисс , ось YY ’ – осью ординат . Точка O их пересечения называется началом координат . На осях координат выбирается произвольный масштаб .
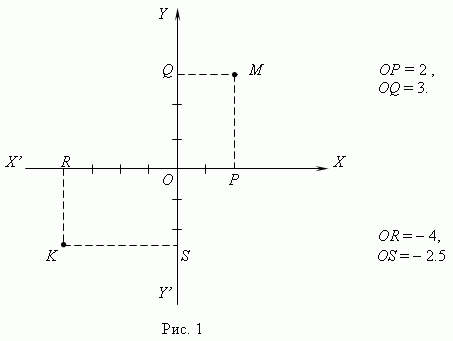
Найдём прекции P и Q точки M на оси координат XX ’ и YY ’ . Отрезок OP на оси XX ’ и число x , измеряющее его длину в соответствии с выбранным масштабом, называется абсциссой точки M ; отрезок OQ на оси YY ’ и число y , измеряющее его длину - ординатой точки M . Величины x = OP и y = OQ называются декартовыми координатами ( или просто – координатами ) точки M . Они считаются положительными или отрицательными в зависимости от принятых положительного и отрицательного направлений осей координат. Положительные абсциссы обычно располагаются на оси XX ’ справа от начала координат; положительные ординаты – вверх по оси YY ’ от начала координат. На рис.1 видно: точка M имеет абсциссу x = 2 и ординату y = 3; точка K имеет абсциссу x = - 4 и ординату y = - 2.5. Это можно записать так: M ( 2, 3 ), K ( - 4, - 2.5 ). Таким образом, каждой точке на плоскости соответствует пара чисел ( x , y ), и наоборот, каждой паре чисел ( x , y ) соответствует одна точка на плоскости.
Графическое представление функций.
Чтобы представить функцию y = f ( x ) в виде графика, нужно:
1) Записать ряд значений функции и её аргумента в таблицу:
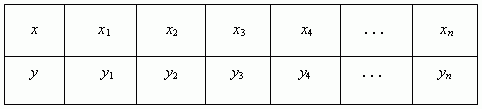
2) Перенести координаты точек функции из таблицы в систему координат,
отметив в соответствии с выбранным масштабом значения абсцисс на
оси Х и значения ординат на оси Y ( рис.2 ). В результате в нашей системе
координат будет построен ряд точек A , B , C , . . . , F .
3) Соединяя точки A , B , C , . . . , F плавной кривой, получаем график заданной
функциональной зависимости.
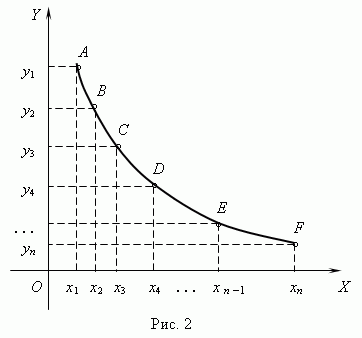
Такое графическое представление функции даёт наглядное представление о характере её поведения, но достигаемая при этом точность недостаточна. Возможно, что промежуточные точки, не построенные на графике, лежат далеко от проведенной плавной кривой. Хорошие результаты в значительной степени зависят также от удачного выбора масштабов. Поэтому следует определить график функции как геометрическое место точек , координаты которых M ( x , y ) связаны заданной функциональной зависимостью .