Геометрическое место точек. Круг и окружность
Геометрическое место точек. Срединный перпендикуляр . Биссектриса угла.
Окружность. Круг . Центр окружности. Радиус. Дуга. Секущая. Хорда.
Диаметр. Касательная и её свойства. Сегмент. Сектор. Углы в круге.
Длина дуги . Радиан. Соотношения между элементами круга.
Геометрическое место точек – это множество всех точек, удовлетворя ющих определённым заданным условиям.
П р и м е р 1. Срединный перпендикуляр любого отрезка есть геометрическое
место точек (т.е. множество всех точек), равноудалён ных от
концов этого отрезка.
Пусть
PO
![]() AB
и
AO = OB :
AB
и
AO = OB :
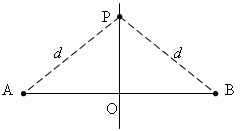
Тогда, расстояния от любой точки P , лежащей на срединном перпендикуляре PO , до концов A и B отрезка AB одинаковы и равны d .
Таким образом, каждая точка срединного перпендикуляра отрезка обладает следующим свойством: она равноудалена от концов отрезка.
П р и м е р 2 . Биссектриса угла есть геометрическое место точек, равноудалённых от его сторон .
П р и м е р 3 . Окружность есть геометрическое место точек (т.е. множе ство
всех точек), равноудалённых от её центра ( на рис. пока зана одна
из этих точек – А ).
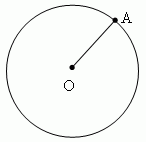
Окружность - это геометрическое место точек (т.е. множество всех точек) на плоскости , равноудалённых от одной точки, называемой центром окружности. Отрезок, соединяющий центр окружности с какой-либо её точкой, называется радиусом и обозначается r или R . Часть плоскости, ограниченная окружностью, называется кругом . Часть
окружности ( A m B , рис.39 ) называется дугой. Прямая PQ , проходящая через точки M и N окружности ( рис.39 ), называется секущей, а её отрезок MN , лежащий внутри окружности - хордой.
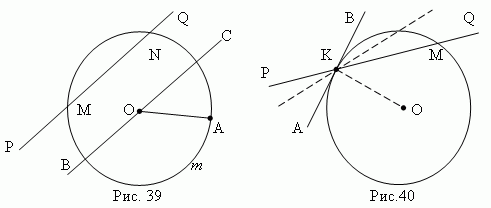
Хорда, проходящая через центр круга ( например, BC , рис.39 ), называется диаметром и обозначается d или D . Диаметр – это наибольшая хорда, равная двум радиусам ( d = 2 r ).
Касательная. Предположим, секущая PQ ( рис.40 ) проходит через точки K и M окружности. Предположим также, что точка M движется вдоль окружности, приближаясь к точке K . Тогда секущая PQ будет менять своё положение, вращаясь вокруг точки K . По мере приближения точки M к точке K секущая PQ будет стремиться к некоторому предельному положению АВ. Прямая AB называется касательной к окружности в точке K . Точка K называется точкой касания. Касательная и окружность имеют только одну общую точку – точку касания.
Свойства касательной.
1)
К
асательная
к окружности перпендикулярна к радиусу, проведенному
в точку касания
(
AB
![]() OK,
рис.40 )
.
OK,
рис.40 )
.
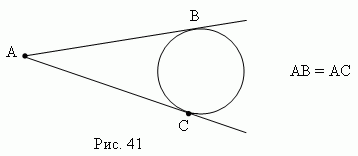
2) Из точки, лежащей вне круга, можно провести две касательные к одной и той же окружности; их отрезки равны ( рис.41 ).
Сегмент – это часть круга, ограниченная дугой ACB и соответствующей хордой AB ( рис.42 ). Длина перпендикуляра CD , проведенного из середины хорды AB до пересечения с дугой ACB , называется высотой сегмента.
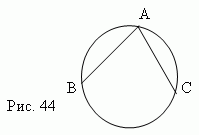
Сектор
–
это
часть круга,
ограниченная дугой
A
m
B
и
двумя радиусами
OA
и
OB
,
![]()
![]() проведенными
к концам этой дуги ( рис.43 ).
проведенными
к концам этой дуги ( рис.43 ).
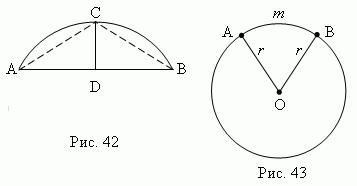
Углы в круге.
Центральный угол
–
угол, образованный двумя
радиусами (
![]() AOB,
рис.43 ).
Вписанный угол
– угол, образованный двумя
хордами
AB
и
AC
, проведенными из
их одной общей точки (
AOB,
рис.43 ).
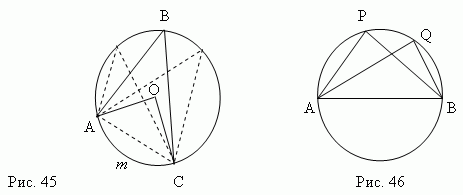
Вписанный угол
– угол, образованный двумя
хордами
AB
и
AC
, проведенными из
их одной общей точки (
![]() BA
C
, рис.44 ).
Описанный
угол
– угол, образованный двумя касательными
AB
и
AC
, проведенными из одной общей точки (
BA
C
, рис.44 ).
Описанный
угол
– угол, образованный двумя касательными
AB
и
AC
, проведенными из одной общей точки (
![]() BAC,
рис.41 ).
BAC,
рис.41 ).
Длина дуги
окружности
пропорциональна её радиусу
r
и соответствующему
центральному углу
![]() :
:
Таким образом, если мы знаем длину дуги l и радиус r , то величина соответствующего центрального угла
Эта формула является основой для
определения
радианного измерения
углов. Так, если
l
=
r
,
то
![]() = 1, и мы говорим, что
угол
= 1, и мы говорим, что
угол
![]() равен
1 радиану (
это обозначается:
равен
1 радиану (
это обозначается:
![]() = 1
рад
). Таким
образом, мы имеем следующее определение радиана как единицы измерения углов:
радиан
– это центральный угол
(
= 1
рад
). Таким
образом, мы имеем следующее определение радиана как единицы измерения углов:
радиан
– это центральный угол
(
![]() AOB,
рис.43 ),
у
которого длина дуги равна её радиусу
(
A
m
B
=
AO
,
рис.43 ).
Итак,
радианная мера любого угла – это отношение длины дуги,
проведенной произвольным радиусом и заключённой между сторонами этого угла, к её
радиусу.
В частности, в соответствии с формулой длины дуги, длина окружности
C
может быть выражена следующим образом:
AOB,
рис.43 ),
у
которого длина дуги равна её радиусу
(
A
m
B
=
AO
,
рис.43 ).
Итак,
радианная мера любого угла – это отношение длины дуги,
проведенной произвольным радиусом и заключённой между сторонами этого угла, к её
радиусу.
В частности, в соответствии с формулой длины дуги, длина окружности
C
может быть выражена следующим образом:
где
![]() определяется как
отношение
C
к диаметру круга 2
r
:
определяется как
отношение
C
к диаметру круга 2
r
:
![]() - иррациональное число; его
приближённое значение
3.1415926…
- иррациональное число; его
приближённое значение
3.1415926…
С другой стороны,
2
![]() - это
круговой угол
окружности, который в градусной
системе измерения равен 360º. На практике часто случается, что как радиус дуги,
так и угол неизвестны. В этом случае длина дуги может быть вычислена по
приближённой формуле Гюйгенса:
- это
круговой угол
окружности, который в градусной
системе измерения равен 360º. На практике часто случается, что как радиус дуги,
так и угол неизвестны. В этом случае длина дуги может быть вычислена по
приближённой формуле Гюйгенса:
где ( см. рис.42 ): p – длина дуги ACB ; l – длина хорды AC ; L – длина хорды AB . Если дуга содержит не более чем 60 º , относительная погрешность этой формулы не превышает 0.5%.
Соотношения между
элементами круга.
Вписанный угол
(
![]() ABC
, рис.45
)
равен половине
центрального угла
,
опирающегося на ту же дугу
A
mC
(
ABC
, рис.45
)
равен половине
центрального угла
,
опирающегося на ту же дугу
A
mC
(
![]() AOC
,
рис.45
)
.
Поэтому,
все
вписанные углы
(
рис.45
),
опирающиеся на одну
и ту
же дугу
(
A
m
C
, рис.45
),
равны.
А так как центральный угол
содержит то
же количество градусов,
что
и его дуга (
A
m
C
,
рис.45
), то
любой вписанный угол измеряется
половиной дуги, на которую он опирается
(
в
нашем случае
A
m
C
).
AOC
,
рис.45
)
.
Поэтому,
все
вписанные углы
(
рис.45
),
опирающиеся на одну
и ту
же дугу
(
A
m
C
, рис.45
),
равны.
А так как центральный угол
содержит то
же количество градусов,
что
и его дуга (
A
m
C
,
рис.45
), то
любой вписанный угол измеряется
половиной дуги, на которую он опирается
(
в
нашем случае
A
m
C
).
Все вписанные углы, опирающиеся на полукруг
(
![]() APB,
APB,
![]() AQB,
…,
рис.46
),
прямые
(
Докажите это, пожалуйста!
).
AQB,
…,
рис.46
),
прямые
(
Докажите это, пожалуйста!
).
Угол
(
![]() AOD,
рис.47
)
, образованный двумя хордами
(
AB
и
CD
),
измеряет
ся
полусуммой дуг, заключённых между его сторонами:
(
A
n
D
+
C
m
B
) / 2 .
AOD,
рис.47
)
, образованный двумя хордами
(
AB
и
CD
),
измеряет
ся
полусуммой дуг, заключённых между его сторонами:
(
A
n
D
+
C
m
B
) / 2 .
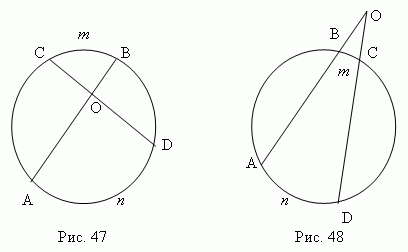
Угол
(
![]() AOD,
рис.48
)
,
образованный двумя секущими
(
AO
и
OD
),
измеряется
полуразностью дуг,
заключённых между его сторонами:
(
A
n
D
–
B
m
C
)
/
2.
AOD,
рис.48
)
,
образованный двумя секущими
(
AO
и
OD
),
измеряется
полуразностью дуг,
заключённых между его сторонами:
(
A
n
D
–
B
m
C
)
/
2.
Угол
(
![]() DCB,
рис.49
)
, образованный касательной и хордой
(
AB
и
CD
),
изме
ряется
половиной
дуги,
заключённой
внутри
него:
C
m
D
/
2.
DCB,
рис.49
)
, образованный касательной и хордой
(
AB
и
CD
),
изме
ряется
половиной
дуги,
заключённой
внутри
него:
C
m
D
/
2.
Угол
(
![]() BOC,
рис.50
)
,
образованный касательной и
секущей
(
CO
и
BO
),
измеряется
полуразностью
дуг,
заключённых между его
сторонами:
(
B
m
C
–
C
n
D
) / 2 .
BOC,
рис.50
)
,
образованный касательной и
секущей
(
CO
и
BO
),
измеряется
полуразностью
дуг,
заключённых между его
сторонами:
(
B
m
C
–
C
n
D
) / 2 .
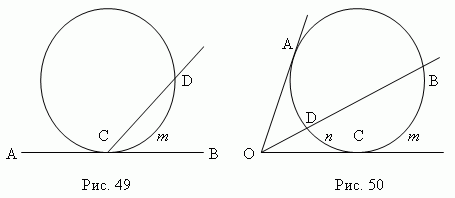
Описанный угол
(
![]() AOC,
рис.50
)
, образованный двумя касательными
(
CO
и
AO
),
измеряется
полуразностью дуг,
заключенных между его
сторонами:
(
ABC
–
CDA
) / 2
.
AOC,
рис.50
)
, образованный двумя касательными
(
CO
и
AO
),
измеряется
полуразностью дуг,
заключенных между его
сторонами:
(
ABC
–
CDA
) / 2
.
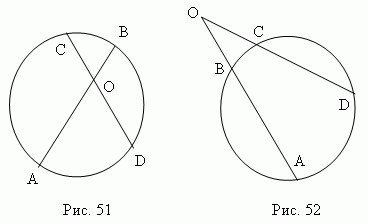
Произведения отрезков хорд ( AB и CD , рис.51 или рис.52 ), на которые они делятся точкой пересечения, равны: AO · BO = CO · DO .
К вадрат касательной равен произведению секущей на её внешнюю часть ( рис.50 ) : OA 2 = OB · O D ( докажите! ). Это свойство можно рассматривать как частный случай рис.52.
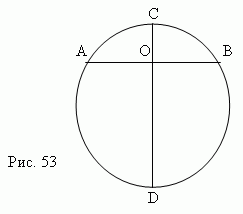
Хорда ( AB , рис.53 ) , перпендикулярная диаметру ( CD ) , делится в их точке пересечения O пополам: AO = OB .
( Попробуйте доказать это! ).