Углы. Проекции. Многогранные углы
Углы между прямыми. Проекции точки и отрезка. Двугранный угол.
Линейный угол. Углы между плоскостями . Многогранный угол.
Углы. Угол между двумя пересекающимися прямыми измеряется так же, как и в планиметрии ( так как через эти прямые можно провести плоскость ). Угол между двумя параллельными прямыми принимается равным 0 или 180 °. Угол между двумя скрещивающимися прямыми AB и CD ( рис.70 ) определяется следующим образом: через любую точку O проводят лучи OM и ON так, что OM || AB и ON || CD . Тогда угол между AB и CD принимается равным углу NOM . Другими словами, прямые AB и CD переносятся в новое положение параллельно самим себе до пересечения. В частности, точка O может быть взята на одной из прямых AB или CD , которая в этом случае будет неподвижной.
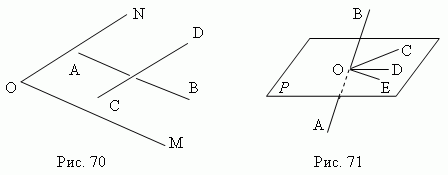
Прямая AB , пересекающая плоскость P в точке O ( рис.71 ), образует ряд углов ( BOC , BOD , BOE ) с различными прямыми OC , OD , OE , проведенными в плоскости P через точку O . Если прямая AB перпендикулярна двум из этих прямых ( например, OC и OE ), то она перпендикулярна ко всем прямым, проведенным в этой плоскости через точку O . В этом случае прямая AB называется перпендикулярной к плоскости Р, а плоскость P – перпендикулярной к прямой AB .
Проекции. Проекцией точки A на плоскость P называется основание C перпендикуляра AC , опущенного из точки A на плоскость P . Проекцией отрезка AB на плоскость P является отрезок CD , концы которого являются проекциями точек A и B ( рис.72 ). Можно спроектировать на плоскость не только пря мую, но и любую кривую ABCDE ( рис.73 ).
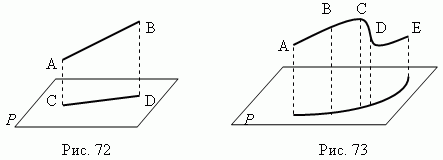
Длины l проекции CD и а отрезка АВ ( рис.72 ) связаны соотношением:
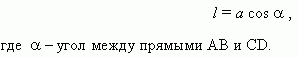
Двугранный угол. Фигура, образованная двумя полуплоскостями Q и R , проходящими через одну и ту же прямую MN ( рис .74 ), называется двугранным углом . Прямая MN называется ребром двугранного угла; полуплоскости Q и R – его гранями . Плоскость P , перпендикулярная к ребру MN , даёт в её пересечении с полуплоскостями Q и R угол AOB . Угол AOB называется линейным углом двугранного угла. Двугранный угол измеряется своим линейным углом.
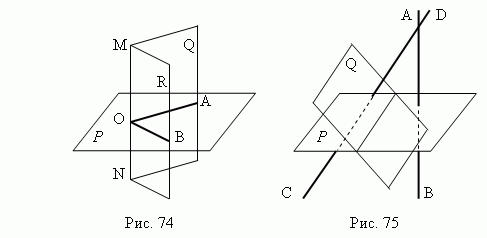
Углы между плоскостями . Две плоскости называются перпендикулярными , если они образуют прямой угол. Угол между двумя параллельными плоскостями принимается равным нулю. В общем случае угол между двумя плоскостями P и Q ( рис.75 ) измеряется углом, образованным прямыми AB и CD , которые перпендикулярны к плоскостям P и Q соответственно.
Многогранный угол. Если через точку O ( рис.76 ) провести множество плоскостей AOB , BOC , COD и т.д., которые последовательно пересекаются друг с другом по прямым OB , OC , OD и т.д. ( последняя из них EOA пересекается с первой AOB по прямой OA ), то мы получим фигуру, называемую многогранным углом. Точка O называется вершиной многогранного угла. Плоскости, образующие многогранный угол ( AOB , BOC , COD , …, EOA ), называются его гранями ; прямые, по которым последовательно пересекаются грани ( OA , OB , OC , … , OE ) называются рёбрами многогранного угла. Углы AOB , BOC , COD , … , EOA называются его плоскими углами . Минимальное количество граней многогранного угла равно 3 ( трёхгранный угол , рис.77 ).
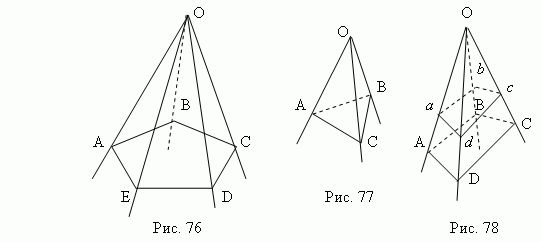
Параллельные плоскости вырезают на рёбрах многогранного угла ( рис.78 ) пропорциональные отрезки ( OA : O a = OB : O b = OC : O c = … ) и образуют подобные многоугольники ( ABCD и abcd ).