Многогранники. Призма, параллелепипед, пирамида
Многогранники. Выпуклый многогранник. Призма.
Прямая, наклонная и правильная призма. Параллелепипед.
Прямой и прямоугольный параллелепипед, куб. Пирамида.
Тетраэдр. Правильная пирамида. Усеченная пирамида.
Многогранник – это тело, граница которого состоит из кусков плоскостей ( многоугольников ) . Эти многоугольники называются гранями , их стороны – рёбрами, их вершины – вершинами многогранника. Отрезки, соединяющие две вершины и не лежащие на одной грани, называются диагоналями многогранника. Многогранник – выпуклый , если все его диагонали расположены внутри него.
Призма – это многогранник ( рис.79 ), две грани которой ABCDE и abcde ( основания призмы ) – равные многоугольники с соответственно параллельными сторонами, а остальные грани ( A ab B , B bc C и т.д. ) - параллелограммы, плоскости которых параллельны прямой ( A a , или B b , или C c и т.д. ). Параллелограммы A ab B , B bc C и т.д. называются боковыми гранями ; рёбра A a , B b , C c и т.д. называются боковыми рёбрами. Высота призмы – это любой перпендикуляр, опущенный из любой точки основания на плоскость другого основания. В зависимости от формы многоугольника, лежащего в основании, призма может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Если боковые рёбра призмы перпендикулярны к плоскости основания, то такая призма называется прямой ; в противном случае – это наклонная призма . Если в основании прямой призмы лежит правильный многоугольник , то такая призма также называется правильной . На рис.79 показана наклонная призма.
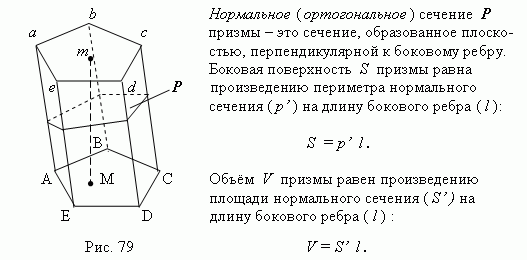
Параллелепипед - это призма, основания которой параллелограммы. Таким образом, параллелепипед имеет шесть граней и все они – параллелограммы. Противоположные грани попарно равны и параллельны. У параллелепипеда
четыре диагонали; они все пересекаются в одной точке и делятся в ней пополам. Если четыре боковые грани параллелепипеда – прямоугольники, то он называется прямым . Прямой параллелепипед, у которого все шесть граней – прямоугольники, называется прямоугольным . Диагональ прямоугольного параллелепипеда d и его рёбра a , b , c связаны соотношением: d 2 = a 2 + b 2 + c 2 . Прямоугольный параллелепипед, все грани которого квадраты, называется кубом . Все рёбра куба равны.
Пирамида – это многогранник, у которого одна грань ( основание пирамиды ) – это произвольный многоугольник ( ABCDE , рис.80 ), а остальные грани ( боковые грани ) – треугольники с общей вершиной S , называемой вершиной пирамиды . Перпендикуляр SO , опущенный из вершины пирамиды на её основание, называется высотой пирамиды . В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром ( четырёхгранником ), четырёхугольная – пятигранником и т.д. Пирамида называется правильной , если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани – равнобедренные треугольники. Высота боковой грани ( SF ) называется апофемой правильной пирамиды.
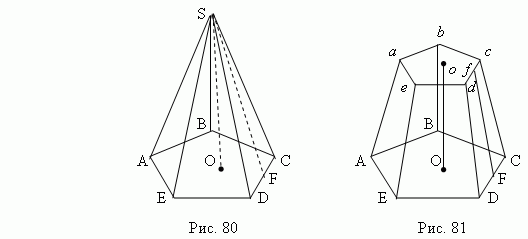
Если провести сечение abcde , параллельное основанию ABCDE ( рис.81 ) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями ; расстояние O o между ними – высотой . Усечённая пирамида называется правильной , если пирамида, из которой она была получена – правильная . Все боковые грани правильной усечённой пирамиды – равные равнобочные трапеции. Высота F f боковой грани ( рис.81 ) называется апофемой правильной усечённой пирамиды.