Шар ( сфера )
Сферическая поверхность. Шар (сфера). Сечения шара: круги.
Теорема Архимеда. Части шара: шаровой (сферический) сегмент,
шаровой слой, шаровой пояс, шаровой сектор.
Сферическая поверхность – это геометрическое место точек ( т.е. множе ство всех точек ) в пространстве, равноудалённых от одной точки O , которая называется центром сферической поверхности ( рис.90 ). Радиус AO и диаметр AB определяются так же, как и в окружности.
Шар ( сфера ) - это тело, ограниченное сферической поверхностью. Можно получить шар, вращая полукруг ( или круг ) вокруг диаметра. Все плоские сечения шара – круги ( рис.90 ). Наибольший круг лежит в сечении, проходящем через центр шара, и называется большим кругом . Его радиус равен радиусу шара. Любые два больших круга пересекаются по диаметру шара ( AB , рис.91 ). Этот диаметр является и диаметром пересекающихся больших кругов. Через две точки сферической поверхности, расположенные на концах одного диаметра ( A и B , рис.91 ), можно провести бесчисленное множество больших кругов. Например, через полюса Земли можно провести бесконечное число меридианов.
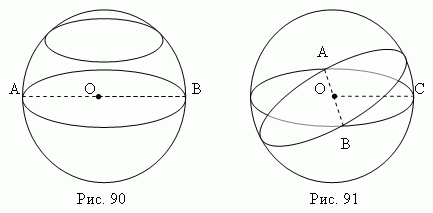
Объём шара в полтора раза меньше объёма описанного вокруг него цилиндра ( рис.92 ), а поверхность шара в полтора раза меньше полной поверхности того же цилиндра ( теорема Архимеда ):
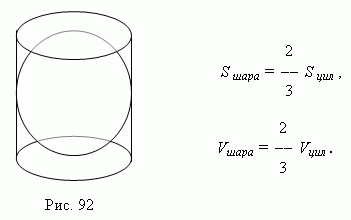
Здесь S шара и V шара - соответственно поверхность и объём шара;
S цил и V цил - полная поверхность и объём описанного цилиндра.
Части шара. Часть шара ( сферы ), отсекаемая от него какой-либо плоскостью ( ABC , рис.93 ), называется шаровым ( сферическим ) сегментом . Круг ABC называется основанием шарового сегмента. Отрезок MN перпендикуляра, проведенного из центра N круга ABC до пересечения со сферической поверхностью, называется высотой шарового сегмента. Точка M называется вершиной шарового сегмента.
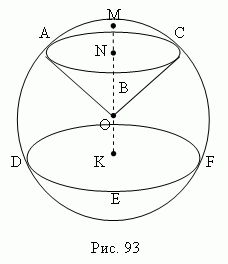
Часть сферы, заключённая между двумя параллельными плоскостями ABC и DEF , пересекающими сферическую поверхность ( рис.93 ), называется шаровым слоем ; кривая поверхность шарового слоя называется шаровым поясом ( зоной ). Круги ABC и DEF – основания шарового пояса. Расстояние NK между основаниями шарового пояса – его высота . Часть шара, ограниченная кривой поверхностью сферического сегмента ( AMCB , рис.93 ) и конической поверхностью OABC , основанием которой служит основание сегмента ( ABC ), а вершиной – центр шара O , называется шаровым сектором .