Касательная плоскость шара, цилиндра и конуса
Касательная плоскость шара, цилиндра и конуса .
Цилиндр, вписанный в призму. Цилиндр, описанный около призмы.
Конус, вписанный в пирамиду. Конус, описанный около пирамиды.
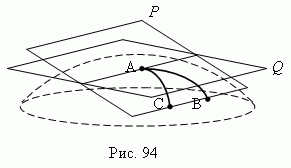
Рассмотрим три точки A , B , C на некоторой кривой поверхности ( рис.94 ) и проведём через них секущую плоскость P . Две точки B и C будем двигать к точке A по двум различным направлениям. Тогда, плоскость P будет стремиться к некоторому предельному положению Q независимо от места, где были взяты точки B и C , и пути их движения к точке A . Плоскость Q называется касательной плоскостью в точке A . Возможно, что в некоторой точке поверхности не существует касательной плоскости. Например, коническая поверхность не имеет касательной плоскости в вершине конуса.
Плоскость P , которая является касательной плоскостью сферической поверхности ( рис.95 ), перпендикулярна к радиусу OA , проведенному в точку касания A ; касательная плоскость сферической поверхности имеет только одну общую точку с этой поверхностью – точку касания.
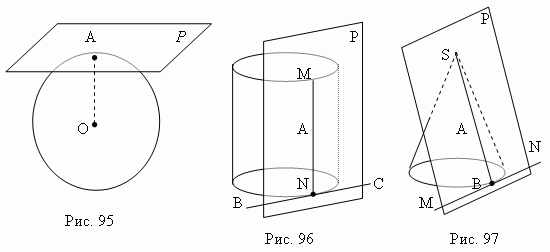
Плоскость P , являющаяся касательной к поверхности круглого цилиндра в точке A ( рис.96 ), проходит через образующую MN , содержащую точку A , и касательную BC круга в основании, содержащую точку N . Плоскость, касательная к поверхности круглого цилиндра удалена от всех точек его оси на расстояние, равное радиусу основания цилиндра. Плоскость P , являющаяся касательной к поверхности круглого конуса в точке A , не совпадающей с вершиной S ( рис.97 ), проходит через образующую SB , содержащую точку A , и касательную MN круга в основании, содержащую точку B . Цилиндр называется вписанным в призму , если боковые грани призмы – плоскости, касательные к цилиндру, а плоскости их оснований совпадают. Цилиндр называется описанным около призмы , если боковые рёбра призмы являются образующими боковой поверхности цилиндра, а плоскости их оснований совпадают. Конус называется вписанным в пирамиду , если боковые грани пирамиды - плоскости, касательные к конусу, а плоскости их оснований совпадают. Конус называется описанным около пирамиды , если боковые рёбра пирамиды являются образующими боковой поверхности конуса, а плоскости их оснований совпадают.