Подобие плоских фигур. Признаки подобия треугольников
Подобие плоских фигур. Отношение подобия.
Подобие многоугольников. Признаки подобия треугольников .
Подобие плоских фигур. Если изменить ( увеличить или уменьшить ) все размеры плоской фигуры в одно и то же число раз ( отношение подобия ), то старая и новая фигуры называются подобными. Например, картина и её фотография – это подобные фигуры.
В
двух подобных фигурах любые соответственные углы равны, то есть, если точки
A
,
B
,
C
,
D
одной фигуры соответствуют точкам
a
,
b
,
c
,
d
другой фигуры, то
ABC =
abc
,
BCD =
bcd
и
т.д.
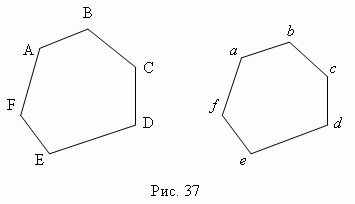
Два многоугольника
(
ABCDEF
и
abcdef
,
рис.37
)
подобны, если их углы равны:
A =
a,
B =
b, …,
F =
f ,
а стороны пропорциональны:
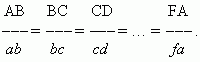
Для подобия многоугольников недостаточно только пропорциональности сторон . Например, квадрат ABCD и ромб abcd ( рис.38 ) имеют пропорциональные стороны: каждая сторона квадрата вдвое больше, чем у ромба,
однако их диагонали не пропорциональны.
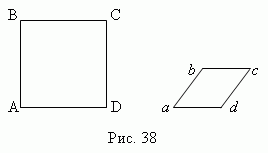
Но для подобия треугольников достаточно пропорциональности их сторон.
Признаки подобия треугольников. Два треугольника подобны, если:
| 1) |
все
их соответственные углы равны (достаточно равенства двух углов);
|
| 2) |
все
их стороны пропорциональны;
|
| 3) |
две стороны одного треугольника пропорциональны двум сторонам другого, a углы, заключённые между этими сторонами, равны. |
Два прямоугольных треугольника подобны, если:
| 1) |
их
катеты пропорциональны;
|
| 2) |
кае катет и гипотенуза одного
треугольника пропорциональны
катету и гипотенузе другого;
|
| 3) | два угла одного треугольника равны двум углам другого. |
Площади подобных фигур пропорциональны квадратам их сходственных линий ( например , сторон ). Так, площади кругов пропорциональны отно шению квадратов их диаметров ( или радиусов ).
| П р и м е р . |
Круглый металлический диск диаметром 20 см весит 6.4 кг. Сколько весит круглый металлический диск диаметром 10 см? |
| Р е ш е н и е . |
Так как малый диск имеет ту же толщину и состоит из того же материала, что и большой, то их веса пропорциональны их площадям, а отношение площади малого диска к площади большого равно :
( 10 / 20 ) 2 = 0.25 . Следовательно, малый диск весит 6.4 · 0.25 = 1.6 кг.
|