Случайные величины
Случайная величина. Дискретные и непрерывные случайные величины.
Независимые случайные величины. Плотность распределения.
Функция распределения. Общие свойства функции распределения.
Переменная величина называется случайной , если в результате опыта она может принимать действительные значения с определёнными вероятностями.
Случайная величина Х называется дискретной , если существует такая неотрицательная функция
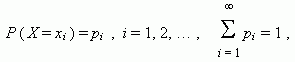
которая ставит в соответствие значению х i переменной Х вероятность р i , с которой она принимает это значение. Дискретные случайные величины X и Y называются независимыми , если события Х = х i и Y = y j при произвольных i и j являются независимыми.
Случайная величина Х называется непрерывной , если для любых a < b существует такая неотрицательная функция f ( x ), что
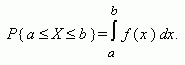
Функция f ( x ) называется плотностью распределения непрерывной случайной величины.
Вероятность того, что случайная величина Х принимает значение меньшее х , называется функцией распределения случайной величины Х и обозначается F ( x ) :
F
(
x
) =
Р
(
X
![]() x
) .
x
) .
Общие свойства функции распределения:
