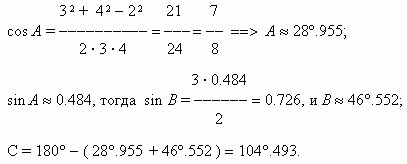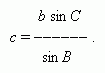Решение косоугольных треугольников


Случай 1.

Заданы три стороны a , b , c . Найти углы A , B , C .

По теореме косинусов находим один из углов: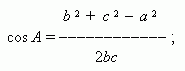



второй угол находим по теореме синусов: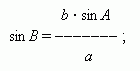

третий угол находится по формуле: C = 180° – ( A + B ).

П р и м е р .

Заданы три стороны треугольника: a = 2, b = 3, c = 4.

Найти его углы.

Р е ш е н и е .

Случай 2.

Дано: две стороны a и b и угол C между ними. Найти сторону c и углы A и B .

По теореме косинусов находим сторону c :



c 2 = a 2 +  b 2 - 2 ab · cos C ;

а затем по теореме синусов – угол A :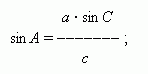

здесь необходимо подчеркнуть, что A – острый угол, если b / a > cos C , и тупой угол, если b / a < cos C . Третий угол B = 180 ° - ( A + C ).

Случай 3.

Заданы любые два угла и сторона. Найти третий угол и две другие стороны.

Очевидно, что третий угол вычисляется по формуле: A + B + C = 180 °, и тогда используя теорему синусов, мы найдём две другие стороны.

Случай 4.

Даны две стороны a и b и угол B , противоположный одной из них. Найти сторону c и углы A и C .

Сначала по теореме синусов найдём угол A :
Здесь возможны следующие случаи:

1) a > b ; a · sin B > b –  здесь решения нет;

2) a > b ; a · sin B = b –  здесь одно решение, A – прямой угол;

3) a > b ; a · sin B < b < a – здесь два решения: A может быть либо острым, либо тупым углом;

4) a b –  здесь одно решение, A – острый угол.

После нахождения угла A , найдём третий угол: C = 180 ° - ( A + B ). Если A может иметь два значения, то и C может иметь два значения. Теперь по теореме синусов можно найти третью сторону:

Если угол C имеет два значения, то и сторона c имеет два значения, следовательно, заданным условиям удовлетворяют два различных треугольника.

П р и м е р . Дано : a = 5, b = 3, B = 30°. Найти сторону c и углы A и C .
Р е ш е н и е .

Здесь: a > b и a sin B < b . ( Проверьте, пожалуйста! ).Тогда согласно случаю 3 здесь возможны два решения:

Назад