Соотношение x = sin y позволяет найти как x по заданному y , так и y по заданному x ( при | x | 1 ). Таким образом, можно рассматривать не только синус как функцию угла, но и угол – как функцию синуса. Этот факт может быть записан как: y = arcsin x ( “ arcsin ” читается “арксинус” ). Например, вместо 1/2 = sin 30 ° можно записать: 30 ° = arcsin 1/2. При второй форме записи угол обычно представляется в радианах: / 6  = arcsin 1/2.

Определения. arcsin x – это угол, синус которого равен x . Аналогично определяются функции arccos x , arctan x , arccot x , arcsec x , arccosec x . Эти функции являются обратными по отношению к функциям sin x , cos x , tan x , cot x , sec x , cosec x , поэтому они называются обратными тригонометрическими функциями. Все обратные тригонометрические функции являются многознач ными функциями , то есть каждому значению аргумента соответствует бесчисленное множество значений функции. Так, например, углы 30 ° , 150 ° , 390 °, 510 °, 750 ° имеют один и тот же синус.

Главное значение arcsin x – это его значение, которое находится между - / 2 и + / 2  ( - 90 ° и + 90 ° ), включая границы :

– / 2 arcsin x + / 2 .

Главное значение arccos x – это его значение, которое находится между 0 и ( 0 ° и + 180 ° ), включая границы :

0 arccos x .

Главное значение arctan x – это его значение, которое находится между - / 2 и + / 2  ( - 9 0 ° и + 90 ° ) без границ :

– / 2  <  arctan x <  + / 2 .

Главное значение arccot x – это его значение, которое находится между 0 и ( 0 ° и + 180 ° ) без границ :

0  <  arccot x < .

Если обозначить любое из значений обратных тригонометрических функций через Arcsin x , Arccos x , Arctan x , Arccot x и сохранить обозначения: arcsin x , arcos x , arctan x , arccot x для их главных значений, то связь между ними выражается следующими соотношениями:

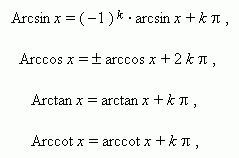
где k – любое целое число. При k = 0  мы имеем главные значения.