Тригонометрические уравнения. Основные методы решений

Тригонометрические уравнения .

Простейшие тригонометрические уравнения .

Методы решения тригонометрических уравнений.

Тригонометрические уравнения. Уравнение, содержащее неизвестное под знаком тригонометрической функции, называется тригонометрическим .

Простейшие тригонометрические уравнения.







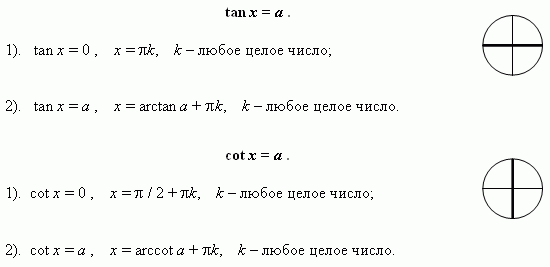
Методы решения тригонометрических уравнений. Решение тригонометрического уравнения состоит из двух этапов: преобразование уравнения для получения его простейшего вида ( см. выше ) и решение полученного простейшего тригонометрического уравнения. Существует семь основных методов решения  тригонометрических уравнений.

1. Алгебраический метод. Этот метод нам хорошо известен из алгебры

( метод замены переменной и подстановки ).

2. Разложение на множители. Этот метод рассмотрим на примерах.

П р и м е р  1.  Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е .   Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

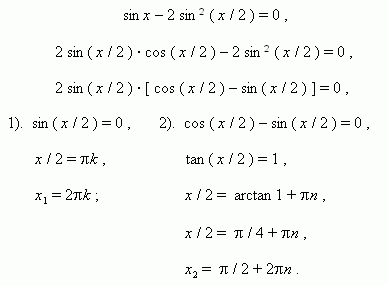
П р и м е р   2.   Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

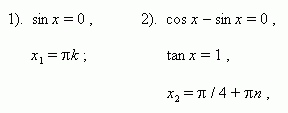
П р и м е р   3.   Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4 x cos 2 x = 2 cos ² 4 x ,

cos 4 x · ( cos 2 x –  cos 4 x ) = 0 ,

cos 4 x · 2 sin 3 x · sin x = 0 ,

1).  cos 4 x = 0 ,               2).  sin 3 x = 0 ,          3). sin x = 0 ,

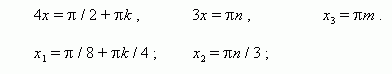
3.

Приведение к однородному уравнению. Уравнение называется однородным от носительно sin и cos , если все его члены одной и той же степени относительно sin и cos одного и того же угла . Чтобы решить однородное уравнение, надо:

а )  перенести все его члены в левую часть;

б )  вынести все общие множители за скобки;

в )  приравнять все множители и скобки нулю;

г )  скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д )  решить полученное алгебраическое уравнение относительно tan .

П р и м е р .   Решить уравнение:  3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4 y +3 = 0 ,

корни этого уравнения: y 1 = - 1, y 2 = - 3,  отсюда

1)   tan x = –1, 2)   tan x = –3,

4. Переход к половинному углу. Рассмотрим этот метод на примере:

П р и м е р .  Решить уравнение:  3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

.   .   .   .   .   .   .   .   .   .

5. Введение вспомогательного угла. Рассмотрим уравнение вида :

a sin x + b cos x = c ,

где a , b , c – коэффициенты; x – неизвестное.

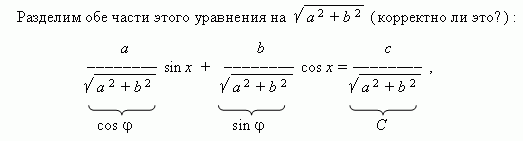
Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого

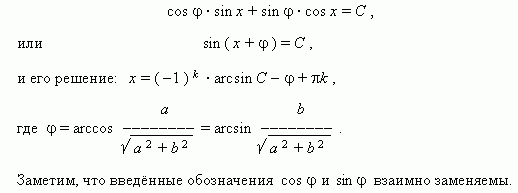
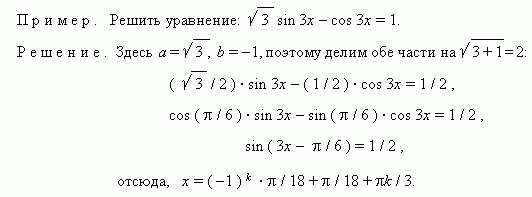
из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь - так называемый вспомогательный угол ), и наше уравнение прини мает вид:

6. Преобразование произведения в сумму. Здесь используются соответствующие формулы.

П р и м е р . Решить уравнение:  2 sin 2 x · sin 6 x = cos 4 x .

Р е ш е н и е .  Преобразуем левую часть в сумму:

cos 4 x – cos 8 x = cos 4 x ,

cos 8 x = 0 ,

8 x = p / 2 + p k ,

x = p / 16 + p k / 8 .

7. Универсальная подстановка. Рассмотрим этот метод на примере.

П р и м е р . Решить уравнение:  3 sin x – 4 cos x = 3 .

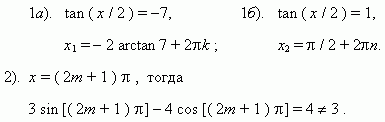
Таким образом, решение даёт только первый случай.

Назад