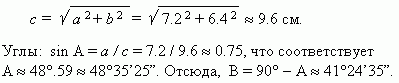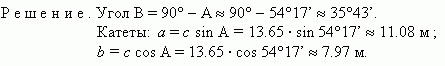Решение прямоугольных треугольников
По двум сторонам. По стороне и острому углу.
| 1. |
По двум сторонам.
Если заданы две стороны прямоугольного треугольника, то третья сторона вычисляется по теореме
Пифагора (см.
соответствующий параграф в разделе «Треугольник» главы «Геометрия»
).
Острые углы могут быть определены поодной из трёх первых формул для тригонометрических функций в зависимости от того, какие стороны известны.
Например, если заданы катеты
a
и
b
, то угол A определяется по формуле:
tan A =
a / b
.
Катет
a
= 0.324, гипотенуза
c
= 0.544. Найти второй катет
b
и углы
A
и
B
.
Даны два катета:
a
= 7.2 см,
b
= 6.4 см. Найти гипотенузу
и углы
A
и
B
.
|
||||||||
| 2. |
По стороне и
острому углу.
Если
задан
один
острый
угол
A
,
то
другой
острый
угол
B
находится из равенства:
B
= 90
° - A.
Стороны находятся по
формулам
тригонометрических
функций, переписанных в виде:
Остаётся выбрать те формулы,
которые содержат заданную или уже найден
ную
сторону.
|
||||||||