Тригонометрические функции любого угла
Единичный круг. Отсчет углов в единичном круге.
Отрицательные и положительные углы.
Четверти единичного круга.
Линии синуса и косинуса. Синус. Косинус.
Знаки синуса и косинуса в различных четвертях единичного круга.
Линии тангенса и котангенса. Тангенс. Котангенс.
Знаки тангенса и котангенса в различных четвертях единичного круга.
Секанс. Косеканс.
Чтобы построить всю тригонометрию, законы которой были бы справедливы для любых углов ( не только для острых, но и для тупых, положительных и отрицательных углов ), необходимо рассмотреть так называемый единичный круг , то есть круг, радиус которого равен 1 ( рис.3 ).
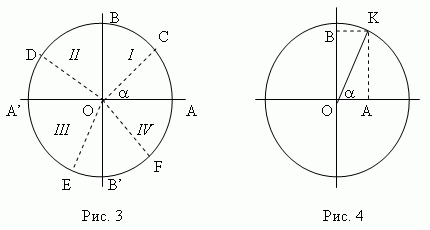
Проведём два диаметра:
горизонтальный
AA
’
и вертикальный
BB
’.
Будем отсчитывать
углы
от
точки
A
(
начальная точка
).
Отрицательные
углы
отсчитываются
по
часовой
стрелке
,
положительные
–
против
.
Подвижный радиус
OC
образует
угол
![]() с
неподвижным
радиусом
OA
.
Он
может
быть
расположен в
1-ой
четверти (
COA
), во 2-ой четверти (
DOA
), в 3-ей четверти (
EOA
) или в 4-ой четверти
(
FOA
). Считая
OA
и
OB
положительными направлениями, а
OA
’
и
OB
’
– отрицательными, мы определим тригонометрические функции следующим образом.
с
неподвижным
радиусом
OA
.
Он
может
быть
расположен в
1-ой
четверти (
COA
), во 2-ой четверти (
DOA
), в 3-ей четверти (
EOA
) или в 4-ой четверти
(
FOA
). Считая
OA
и
OB
положительными направлениями, а
OA
’
и
OB
’
– отрицательными, мы определим тригонометрические функции следующим образом.
Линия синуса
угла
![]() (
рис.4
)
-
это
вертикальный
диаметр единичного круга,
линия
косинуса
угла
(
рис.4
)
-
это
вертикальный
диаметр единичного круга,
линия
косинуса
угла
![]() -
горизонтальный
диаметр единичного
круга.
Синус
угла
-
горизонтальный
диаметр единичного
круга.
Синус
угла
![]() (
рис.4
) – это
отрезок
OB
на линии
синуса,
то
есть
проекция
подвижного
радиуса
OK
на
линию
синуса;
косинус
угла
(
рис.4
) – это
отрезок
OB
на линии
синуса,
то
есть
проекция
подвижного
радиуса
OK
на
линию
синуса;
косинус
угла
![]() -
отрезок
OA
линии косинуса,
то
есть проекция подвижного
радиуса
OK
на линию косинуса.
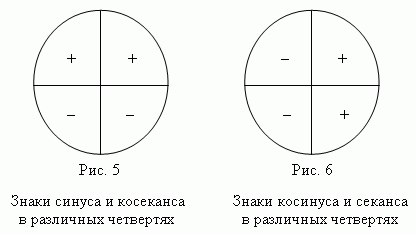
Знаки синуса и косинуса в
различных четвертях единичного круга показаны
на рис.5 и рис.6.
-
отрезок
OA
линии косинуса,
то
есть проекция подвижного
радиуса
OK
на линию косинуса.
Знаки синуса и косинуса в
различных четвертях единичного круга показаны
на рис.5 и рис.6.
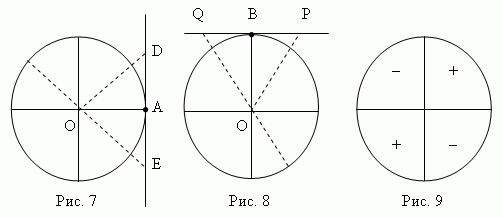
Линия тангенса ( рис.7 ) – это касательная к единичному кругу, проведенная через точку A горизонтального диаметра.
Линия котангенса ( рис.8 ) – это касательная к единичному кругу, проведенная через точку В вертикального диаметра.
Тангенс – это отрезок линии тангенса между точкой касания A и точкой пересечения ( D , E , и т.д., рис.7 ) линии тангенса и линии радиуса.
Котангенс – это отрезок линии котангенса между точкой касания В и точкой пересечения ( Р, Q , и т.д., рис.8 ) линии котангенса и линии радиуса.
Знаки тангенса и котангенса в различных четвертях единичного круга показаны на рис.9.
Секанс и косеканс определяются как величины, обратные соответственно косинусу и синусу.