Логарифмом положительного числа N по основанию ( b > 0, b 1 ) называется показатель степени x , в которую нужно возвести b , чтобы получить N .

Обозначение логарифма:

Эта запись равнозначна следующей: b ^x = N .

П р и м е р ы : log ₃ 81 = 4 , так как  3 ⁴ = 81 ;

log _1/3 27 = – 3 , так как  ( 1/3 ) ^{- 3} = 3 ³ = 27 .

Вышеприведенное определение логарифма можно записать в виде тождества:

Основные свойства логарифмов.

1) log b = 1 , так как b ¹ = b .

b

2) log 1 = 0 , так как b ⁰ = 1 .

b

3) Логарифм произведения равен сумме логарифмов сомножителей:

log ( ab ) = log a + log b .

4) Логарифм частного равен разности логарифмов делимого и делителя:

log ( a / b ) = log a – log b .

5) Логарифм степени равен произведению показателя степени на логарифм её основания:

log ( b ^k ) = k · log b .

Следствием этого свойства является следующее: логарифм корня равен логарифму подкоренного числа, делённому на степень корня:

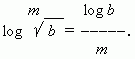
6) Если в основании логарифма находится степень, то величину, обратную показателю степени, можно вынести за знак лога рифма:

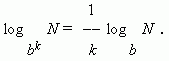
Два последних свойства можно объединить в одно:

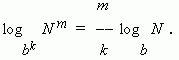
7) Формула модуля перехода ( т. e . перехода от одного основания логарифма к другому основанию ):

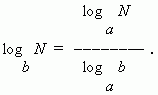
В частном случае при N = a имеем:

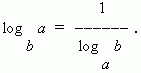
Десятичным логарифмом называется логарифм по основанию 10. Он обозначается lg , т.е. log ₁₀ N = lg N . Логарифмы чисел 10, 100, 1000, ... p авны соответственно 1,  2,  3, …, т.е. имеют столько положительных

единиц, сколько нулей стоит в логарифмируемом числе после единицы. Логарифмы чисел 0.1, 0.01, 0.001, ... p авны соответственно –1, –2, –3, …, т.е. имеют столько отрицательных единиц, сколько нулей стоит в логарифмируемом числе перед единицей ( считая и нуль целых ). Логарифмы остальных чисел имеют дробную часть, называемую мантиссой . Целая часть логарифма называется характеристикой . Для практического при менения десятичные логарифмы наиболее удобны.

Натуральным логарифмом называется логарифм по основанию е . Он обозначается ln , т.е. log _e N = ln N . Число е является иррациональным, его приближённое значение 2.718281828. Оно является пределом, к которому стремится число ( 1 + 1 / n ) ⁿ при неограниченном возрастании n ( см. первый замечательный предел на странице "Пределы числовых последовательностей" ).
Как это ни покажется странным, натуральные логарифмы оказались очень удобными при проведении различного рода операций, связанных с анализом функций. Вычисление логарифмов по основанию е осуществляется гораздо быстрее, чем по любому другому основанию.

Назад