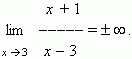Пределы функций
Предел функции. Некоторые замечательные пределы.
Бесконечно малая и бесконечно большая величины.
Конечный предел. Бесконечный предел.
Понятие бесконечности.
Предел функции.
Число
L
называется пределом функции
y
=
f
(
x
)
при
x
, стремящемся к
a
:
если для любого
>
0
найдётся такое положительное число
=
(
),
зависящее от
,
что
из условия
|
x
-
a
|
<
с
ледует
|
f
(
x
) –
L
| <
.
Это определение означает, что L есть предел функции y = f ( x ), если значение функции неограниченно приближается к
L , когда значение аргумента x приближается к a . Геометрически это значит, что для любого
>
0
можно найти такое число
,
что если
x
находится в интервале (
a
-
,
a
+
), то значение функции лежит в интервале (
L
-
,
L
+
). Отметим, что в соответствии с этим определением
аргумент функции лишь
приближается
к
a
, не принимая этого значения! Это следует учитывать при
вычислении предела любой функции в точке её разрыва
,
где функция не существует.
П р и м е р . Найти
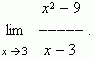
Р е ш е н и е . Подставляя
x = 3 в выражение
получим не
имеющее
смысла
выражение
(
см. пункт
"О выражениях, не имеющих смысла"
на стр.
"Степени и корни" в главе "Алгебра"). Поэтому решим по-другому:
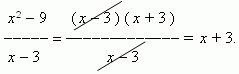
Сокращение дроби в данном случае корректно, так как
x
3 ,
он лишь
приближается
к 3. Теперь мы имеем:
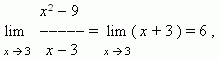
поскольку, если x стремится к 3, то x + 3 стремится к 6 .
Некоторые замечательные пределы.
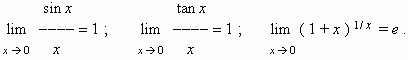
Бесконечно малая и бесконечно большая величины. Если предел некоторой переменной равен 0, то эта переменная называется бесконечно малой .
П р и м е р . Функция
y
=
является бесконечно малой при
x
,
cтремящемся к 4, так как
Если абсолютное значение некоторой переменной неограниченно возрастает, то эта переменная называется бесконечно большой .
Бесконечно большая величина не имеет
конечного
предела, но она имеет так
называемый
бесконечный
предел, что записывается как:
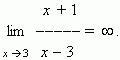
Символ
(
“бесконечность”
)
не
означает
некоторого
числа,
он
означает
только, что
дробь
неограниченно возрастает при
x
, стремящемся к
3.
Следует
отметить,
что
дробь
может
быть
как
положительной
(
при
x
>
3
),
так
и
отрицательной
(
при
x
<
3
). Если бесконечно большая величина может быть только положительной при любых
значениях
x
,
это
отражается в записи.
Например,
при
x
0 функция
y
=
x
-
2
бесконечно большая
,
но
она
положительна как при
x
> 0, так и при
x
< 0 ; это выражается так:
Наоборот, функция y = - x - 2 всегда отрицательна, поэтому
В соответствии с этим, результат в нашем примере можно записать так:
