Основные понятия и свойства функций
Область определения и область значений функции.
Правило (закон) соответствия. Монотонная функция .
Ограниченная и неограниченная функции. Непрерывная и
разрывная функции . Чётная и нечётная функции.
Периодическая функция. Период функции.
Нули функции . Асимптота .
Область определения и область значений функции. В элементарной математике изучаются функции только на множестве действительных чисел R . Это значит, что аргумент функции может принимать только те действительные значения, при которых функция определена, т. e . она также принимает только действительные значения. Множество X всех допустимых действительных значений аргумента x , при которых функция y = f ( x ) определена, называется областью определения функции . Множество Y всех действительных значений y , которые принимает функция, называется областью значений функции . Теперь можно дать более точное определение функции: правило (закон) соответствия между множествами X и Y , по которому для каждого элемента из множества X можно найти один и только один элемент из множества Y , называется функцией .
Из этого определения следует, что функция считается заданной, если:
- задана область определения функции X ;
- задана область значений функции Y ;
- известно правило ( закон ) соответствия, причём такое, что для каждого
значения аргумента может быть найдено только одно значение функции.
Это требование однозначности функции является обязательным.
Монотонная функция. Если для любых двух значений аргумента x 1 и x 2 из условия x 2 > x 1 следует f ( x 2 ) > f ( x 1 ), то функция f ( x ) называется возрастающей ; если для любых x 1 и x 2 из условия x 2 > x 1 следует f ( x 2 ) < f ( x 1 ), то функция f ( x ) называется убывающей . Функция, которая только возрастает или только убывает, называется монотонной .
Ограниченная и неограниченная
функции.
Функция
называется
ограниченной
,
если
существует такое положительное
число
M
,
что |
f
(
x
)
|
M
для
всех значений
x
.
Если такого числа не существует, то функция -
неограниченная
.
П р и м е р ы
.
Функция, изображённая на рис.3, является ограниченной, но не монотонной. Функция на рис.4 - как раз наоборот, монотонная, но неограниченная. ( Объясните это, пожалуйста ! ).
Непрерывная и разрывная функции. Функция y = f ( x ) называется непрерывной в точке x = a , если :
1) функция определена при x = a , т. e . f ( a ) существует;
2) существует конечный предел lim f ( x ) ;
x → a
( см. раздел «Пределы функций» в главе «Основы анализа» )
3) f ( a ) = lim f ( x ) .
x → a
Если не выполняется хотя бы одно из этих условий, то функция называется разрывной в точке x = a .
Если функция непрерывна во всех точках своей области определения , то она называется непрерывной функцией .
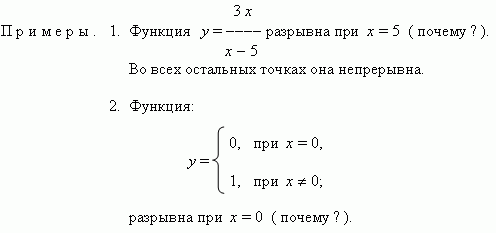
Чётная и нечётная функции. Если для любого x из области определения функции имеет место: f ( - x ) = f ( x ), то функция называется чётной ; если же имеет место : f ( - x ) = - f ( x ), то функция называется нечётной . График чётной функции симетричен относительно оси Y ( рис.5 ), a график нечётной функции сим метричен относительно начала координат ( рис.6 ).
Периодическая функция. Функция f ( x ) - периодическая , если существует такое отличное от нуля число T , что для любого x из области определения функции имеет место: f ( x + T ) = f ( x ). Такое наименьшее число называется периодом функции . Все тригонометрические функции являются периодическими.
П р и м е р
1 . Доказать, что
sin
x
имеет период 2
.
Р е ш е н и е .
Мы знаем, что
sin
(
x
+
2
n
) =
sin
x
,
где
n
= 0,
±
1,
±
2, …
Следовательно, добавление 2
n
к
аргументу синуса не
меняет его значени e . Существует ли другое число с таким
же свойством ?
Предположим, что P – такое число, т. e . равенство:
sin ( x + P ) = sin x ,
справедливо для любого значения x . Но тогда оно имеет
место
и при
x
=
/ 2 , т.
e
.
sin
(
/ 2
+
P
) =
sin
/ 2 = 1.
Но
по
формуле
приведения
sin
(
/ 2
+
P
) =
cos
P
.
Тогда
из двух последних равенств следует, что cos P = 1, но мы
знаем
,
что это верно лишь при
P
=
2
n
.
Так как наименьшим
отличным
от
нуля числом из
2
n
является
2
,
то это число
и есть
период
sin
x
.
Аналогично доказывается, что
2
является периодом и для cos x .
Докажите,
что функции
tan
x
и
cot
x
имеют период
.
П р и м е р 2. Какое число является периодом функции sin 2 x ?
Р е ш е н и е . Рассмотрим
sin 2
x
= sin ( 2
x +
2
n
) = sin [ 2 (
x
+
n
) ] .
Мы видим,
что
добавление
n
к аргументу
x
,
не меняет
значение функции. Наименьшее отличное от нуля число
из
n
есть
,
таким
образом, это период
sin
2
x
.
Нули функции. Значение аргумента, при котором функция равна 0, называется нулём ( корнем ) функции . Функция может иметь несколько нулей. Например, функция y = x ( x + 1 ) ( x - 3 ) имеет три нуля: x = 0, x = - 1, x = 3. Геометрически нуль функции – это абсцисса точки пересечения графика функции с осью Х .
На рис.7 представлен график функции с нулями: x = a , x = b и x = c .
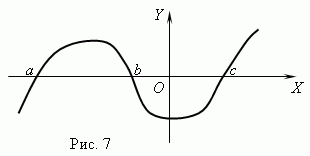
Асимптота. Если график функции неограниченно приближается к некоторой прямой при своём удалении от начала координат, то эта прямая называется асимптотой .