Радианное и градусное измерение углов
Градусная и радианная мера измерения углов.
Соотношение между радиусом и длиной окружности.
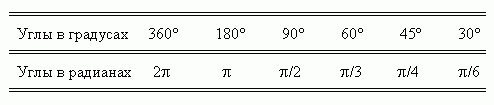
Таблица значений наиболее часто встречающихся углов
в градусах и радианах.
Градусная мера. Здесь единицей измерения является градус ( обозначение ° ) – это поворот луча на 1 / 360 часть одного полного оборота. Таким образом, полный оборот луча равен 360 ° . Один градус состоит из 60 минут ( их обозначение ‘ ); одна минута – соответственно из 60 секунд ( обозначаются “ ) .
Радианная мера.
Как мы знаем из
планиметрии
(
см.
параграф «Длина дуги» в
разделе "Геометрическое место точек. Круг и окружность"»
), длина дуги
l
, радиус
r
и соответствующий центральный угол
связаны
соотношением
:
= l / r .
Эта формула лежит в основе
определения радианной меры измерения углов. Так, если
l
=
r
,
то
= 1, и мы говорим, что угол
равен 1
радиану, что обозначается:
= 1
рад
. Таким образом, мы имеем следующее определение
радианной меры измерения:
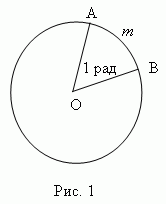
Радиан есть центральный угол, у которого длина дуги и радиус равны ( A m B = AO , рис.1 ). Итак, радианная мера измерения угла есть отношение длины дуги, проведенной произвольным радиусом и заключённой между сторонами этого угла, к радиусу дуги.
Следуя этой формуле, длину окружности C и её радиус r можно выразить следующим образом:
=
C / r .
Так
,
полный оборот, равный 360
°
в градусном измерении, соответствует
2
в
радианном измерении. Откуда мы получаем значение одного радиана:
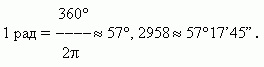
Обратно ,
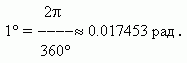
Полезно помнить следующую сравнительную таблицу значений наиболее часто встречающихся углов в градусах и радианах:
